Triangles and Z-Buffer

投影矩阵

透视投影矩阵推导

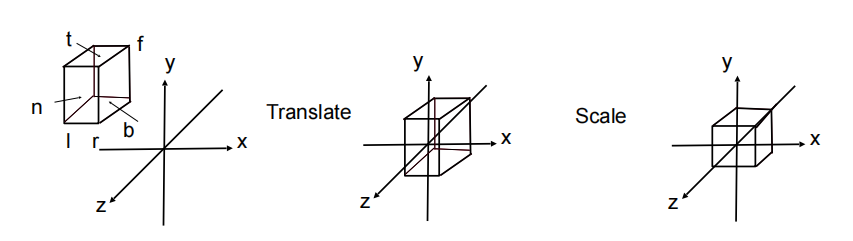
对于正交投影（Orthographic Projection）需要把长方体 进行标准化成正方体，相应的变换矩阵是先进行平移变换（将长方体的中心与原点重合），再进行缩放变换（由于标准化的正方体的边长是 2，长宽高要归一化到 2），即：

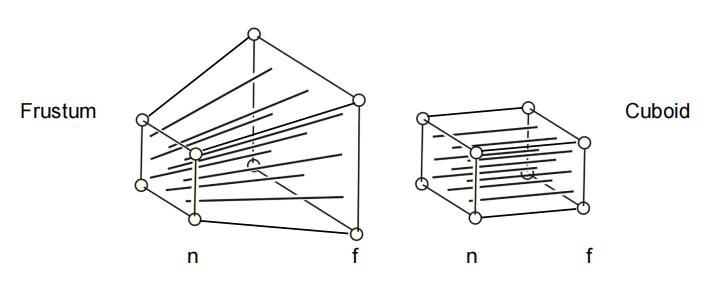
对于透视投影（Perspective Projection），思路是把视锥体“挤压”成长方体，再对长方体进行归一化。于是视锥体内的所有点“挤压”到近平面上（可以想象视角在远平面外侧，方向垂直于远平面），可以根据相似三角形原理计算出“挤压”后的 和坐标

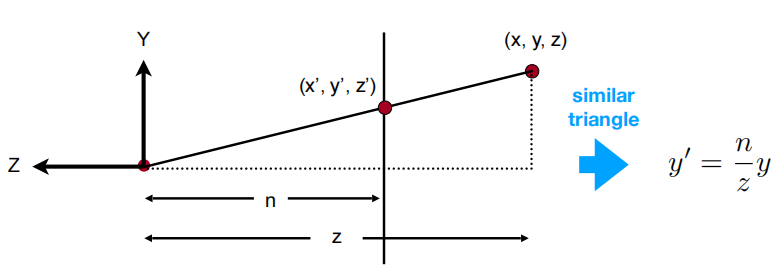
那么“挤压”后的点在齐次坐标系（Homogeneous Coordinates）下可以表示为：

所以从视锥体到长方体的矩阵变换 满足下面的等式：

即

第三行的未知值可以根据两个设定计算出来：

1. 近平面上的任意一点经过“挤压”后的 坐标不发生变化，近平面上的点为 ，挤压后还是，也可以写成，所以第三行一定满足以下等式：
   
   可以得出：
   

2. 远平面上的任意一点经过“挤压”后的 坐标也不会发生变化，同上可得：
   

联立可得：

所以透视投影矩阵可以表示为：

对于函数 get_projection_matrix 中的参数可由下图计算出：

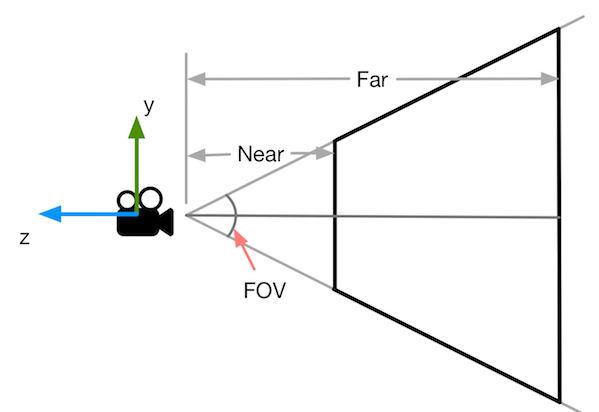
长方体的中心位于原点，则，根据对称性，根据纵横比和对称性可得，，代入公式即可

旋转与投影代码

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar)
{
    // TODO: Copy-paste your implementation from the previous assignment.
    Eigen::Matrix4f projection;
    
    float fov = eye_fov * M_PI / 180.0;
    float t = std::abs(zNear) * std::tan(fov / 2.0);
    float b = -t;
    float r = t * aspect_ratio;
    float l = -r;
    float n = zNear;
    float f = zFar;
    
    Eigen::Matrix4f scale;
    scale << 1 / r - l, 0, 0, 0,
        0, 1 / t - b, 0, 0,
        0, 0, 1 / n - f, 0,
        0, 0, 0, 1;
    
    Eigen::Matrix4f translate;
    translate << 1, 0, 0, 0,
        0, 1, 0, 0,
        0, 0, 1, (n + f) / -2,
        0, 0, 0, 1;
    
    auto orthographic = scale * translate;
    Eigen::Matrix4f orthographicToProjection;
    orthographicToProjection << n, 0, 0, 0,
        0, n, 0, 0,
        0, 0, n + f, -n * f,
        0, 0, 1, 0;
    projection = orthographic * orthographicToProjection;
    
    return projection;
}

三维空间中判断一个点是否在三角形内

1. 求出向量，，
2. 计算，，
3. 如果叉乘后三个向量方向同向则说明 点在三角形内部，否则在外部

static bool insideTriangle(int x, int y, const Vector3f* _v)
{
    // TODO : Implement this function to check if the point (x, y) is inside the triangle represented by _v[0], _v[1], _v[2]
    Eigen::Vector2f side1;
    side1 << _v[1].x() - _v[0].x(), _v[1].y() - _v[0].y();
    Eigen::Vector2f side2;
    side2 << _v[2].x() - _v[1].x(), _v[2].y() - _v[1].y();
    Eigen::Vector2f side3;
    side3 << _v[0].x() - _v[2].x(), _v[0].y() - _v[2].y();
    
    Eigen::Vector2f v1;
    v1 << x - _v[0].x(), y - _v[0].y();
    Eigen::Vector2f v2;
    v2 << x - _v[1].x(), y - _v[1].y();
    Eigen::Vector2f v3;
    v3 << x - _v[2].x(), y - _v[2].y();
    
    float z1 = side1.x() * v1.y() - side1.y() * v1.x();
    float z2 = side2.x() * v2.y() - side2.y() * v2.x();
    float z3 = side3.x() * v3.y() - side3.y() * v3.x();
    
    if ((z1 > 0 && z2 > 0 && z3 > 0) || (z1 < 0 && z2 < 0 && z3 < 0))
    {
        return true;
    }
    else
    {
        return false;
    }
}

光栅化

计算重心坐标

考虑三角形三个顶点 ，， 以及内部坐标点 ，假设又三个值，， 满足：

解方程组可得

static std::tuple<float, float, float> computeBarycentric2D(float x, float y, const Vector3f* v)
{
    float xp = x, yp = y;
    float xa = v[0].x(), ya = v[0].y();
    float xb = v[1].x(), yb = v[1].y();
    float xc = v[2].x(), yc = v[2].y();
    float gamma = ((xb - xa) * (yp - ya) - (xp - xa) * (yb - ya)) / 
                  ((xb - xa) * (yc - ya) - (xc - xa) * (yb - ya));
    float beta = (xp - xa - gamma * (xc - xa)) / (xb - xa);
    float alpha = 1.0f - beta - gamma;
    return {alpha, beta, gamma};
}

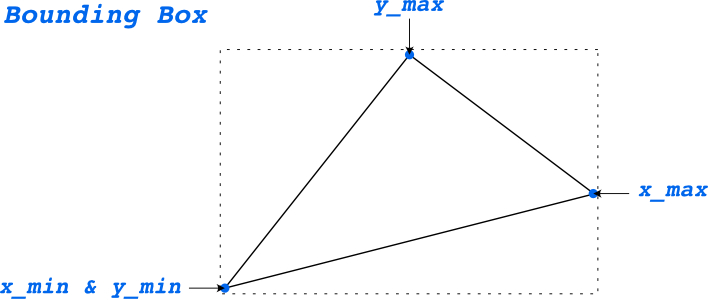
光栅化一个三角形需要扫描三角形所在的包围盒，判断点是否在三角形内部然后通过中心坐标插值

所以判断是否在三角形内部需要加

if (insideTriangle(i + 0.5f, j + 0.5f, t.v)) {
    ...
}

已知重心坐标 ，， 的值求深度值 的公式如下（需要做重心坐标 - 插值校正 ^[1][2]）：

其中，，

重心坐标是在 2D 空间里做的，不能用作插值 3D 空间的坐标，需要经过插值矫正才可以

//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
    auto v = t.toVector4();
    
    // TODO : Find out the bounding box of current triangle.
    // iterate through the pixel and find if the current pixel is inside the triangle
    auto minX = std::min(v[0].x(), std::min(v[1].x(), v[2].x()));
    auto minY = std::min(v[0].y(), std::min(v[1].y(), v[2].y()));
    auto maxX = std::max(v[0].x(), std::max(v[1].x(), v[2].x()));
    auto maxY = std::max(v[0].y(), std::max(v[1].y(), v[2].y()));
    // If so, use the following code to get the interpolated z value.
    // TODO : set the current pixel (use the set_pixel function) to the color of the triangle (use getColor function) if it should be painted.
    for (int i = minX; i <= maxX; i++) {
        for (int j = minY; j <= maxY; j++) {
            if (insideTriangle(i + 0.5f, j + 0.5f, t.v)) {
                float minDepth = FLT_MAX;
                auto tup = computeBarycentric2D(i, j, t.v);
                
                float alpha, beta, gamma;
                std::tie(alpha, beta, gamma) = tup;
                float wReciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
                float zInterpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
                zInterpolated *= wReciprocal;
                minDepth = std::min(minDepth, zInterpolated);
                auto index = get_index(i, j);
                if (depth_buf[index] > minDepth) {
                    Eigen::Vector3f color = t.getColor();
                    Vector3f point;
                    point << i, j, minDepth;
                    depth_buf[index] = minDepth;
                    set_pixel(point, color);
                }
            }
        }
    }
}

---

• [1] 透视投影 - 重心坐标 - 插值校正
• [2] Perspective-Correct Interpolation