红黑树
红黑树
虽然平衡树解决了二叉查找树退化为近似链表的缺点,不过不是最佳方案。因为平衡树要求每个节点的左子树和右子树的高度差至多等于 1,这个要求实在是太严了,导致每次进行插入 / 删除节点的时候,几乎都会破坏平衡树的第二个规则,进而我们都需要通过左旋和右旋来进行调整,使之再次成为一颗符合要求的平衡树。显然,如果在那种插入、删除很频繁的场景中,平衡树需要频繁着进行调整,这会使平衡树的性能大打折扣,为了解决这个问题,于是有了红黑树。 #f8dcf8
红黑树的性质
- 每个节点要么是黑色,要么是红色
- 根节点是黑色
- 每个叶子节点(NIL)是黑色
- 每个红色节点的两个子节点一定都是黑色,不能有两个红色结点相连
- 任意一结点到每个叶子节点的路径都包含数量相同的黑节点
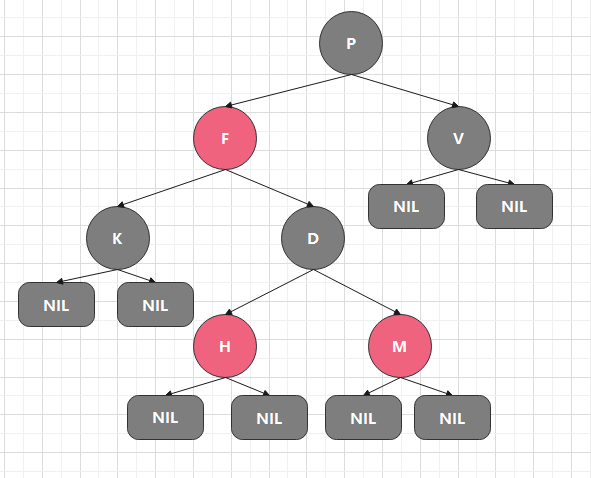
红黑树的数据结构
1 | |
红黑树的时间复杂度
红黑树时间复杂度显然不会为最糟糕的
红黑树保持平衡的三种操作
- 左旋:以某个节点作为指点(旋转节点),其右子节点变为旋转节点的父节点,右子节点的左子节点变为选装节点的右子节点,左子节点保持不变。
- 右旋:以某个节点作为支点(旋转节点),其左子节点变为旋转节点的父节点,左子节点的右子节点变为旋转节点的左子节点,右子节点保持不变。
- 变色:节点的颜色由红变黑或由黑边红。
左旋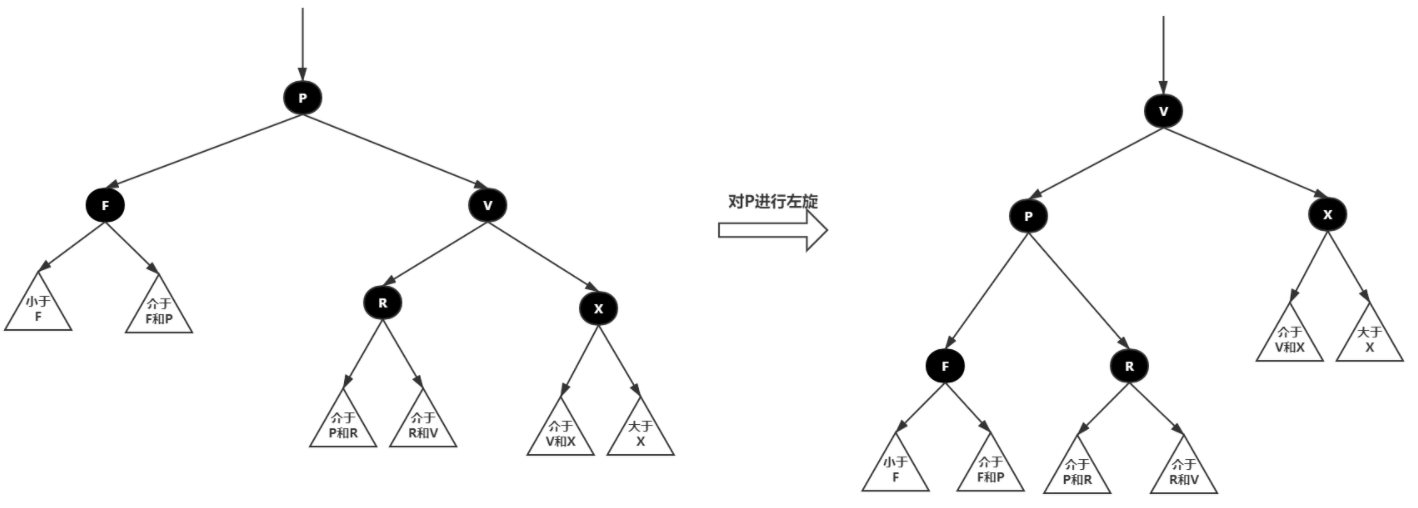
右旋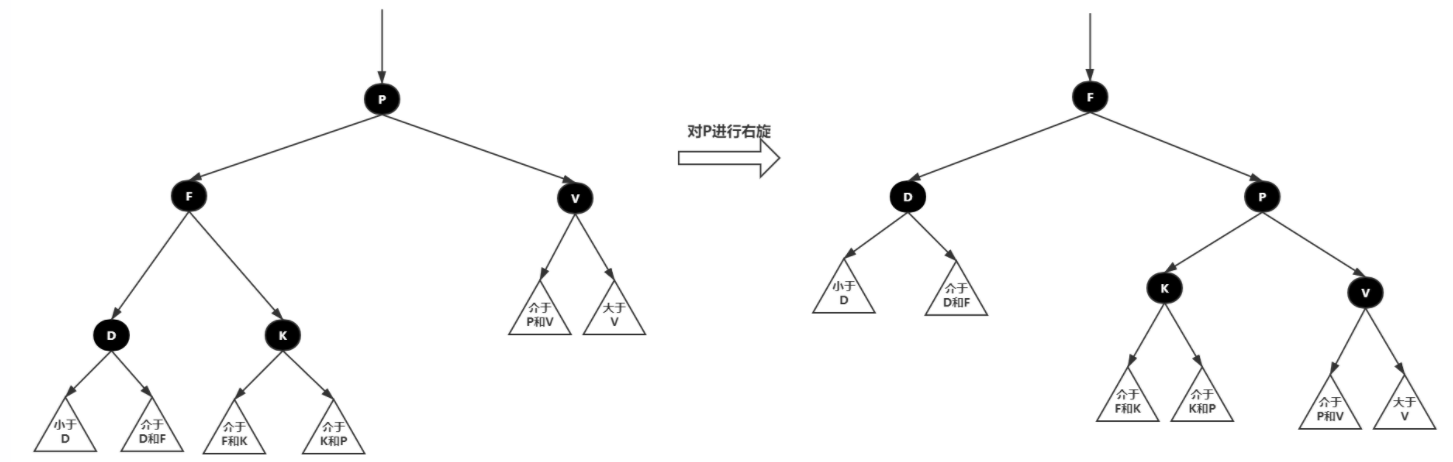
红黑树
https://silhouettesforyou.github.io/2021/11/22/7ac3af061ccd/