Last updated on 2024-08-05T09:36:44+08:00
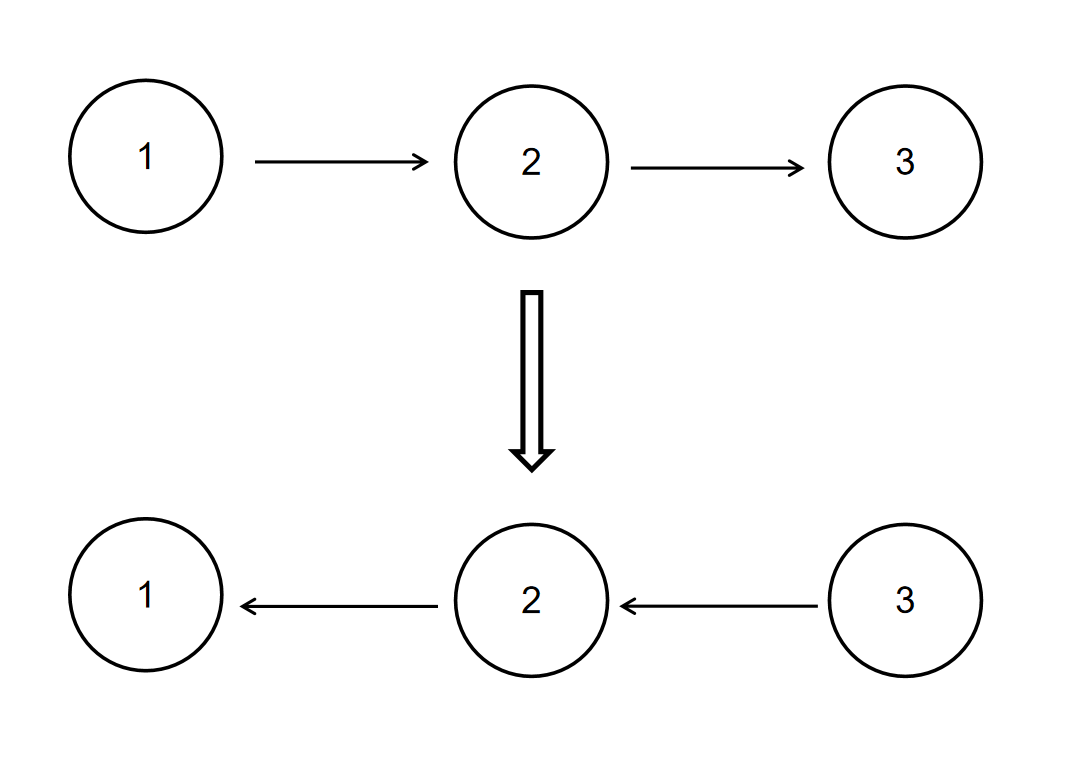
反转链表 描述
数据范围:
要求:空间复杂度
如当输入链表 {1, 2, 3} 时,{3, 2, 1},所以对应的输出为{3, 2, 1}。
Solution 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution {public :ListNode* ReverseList (ListNode* head) {if (head == nullptr || head->next == nullptr )return head;auto p = head->next;nullptr ;while (p) {auto q = p->next;return head;
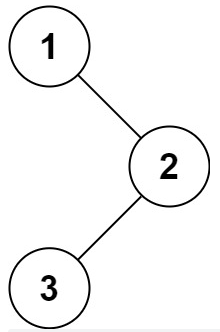
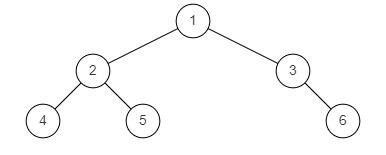
二叉树遍历
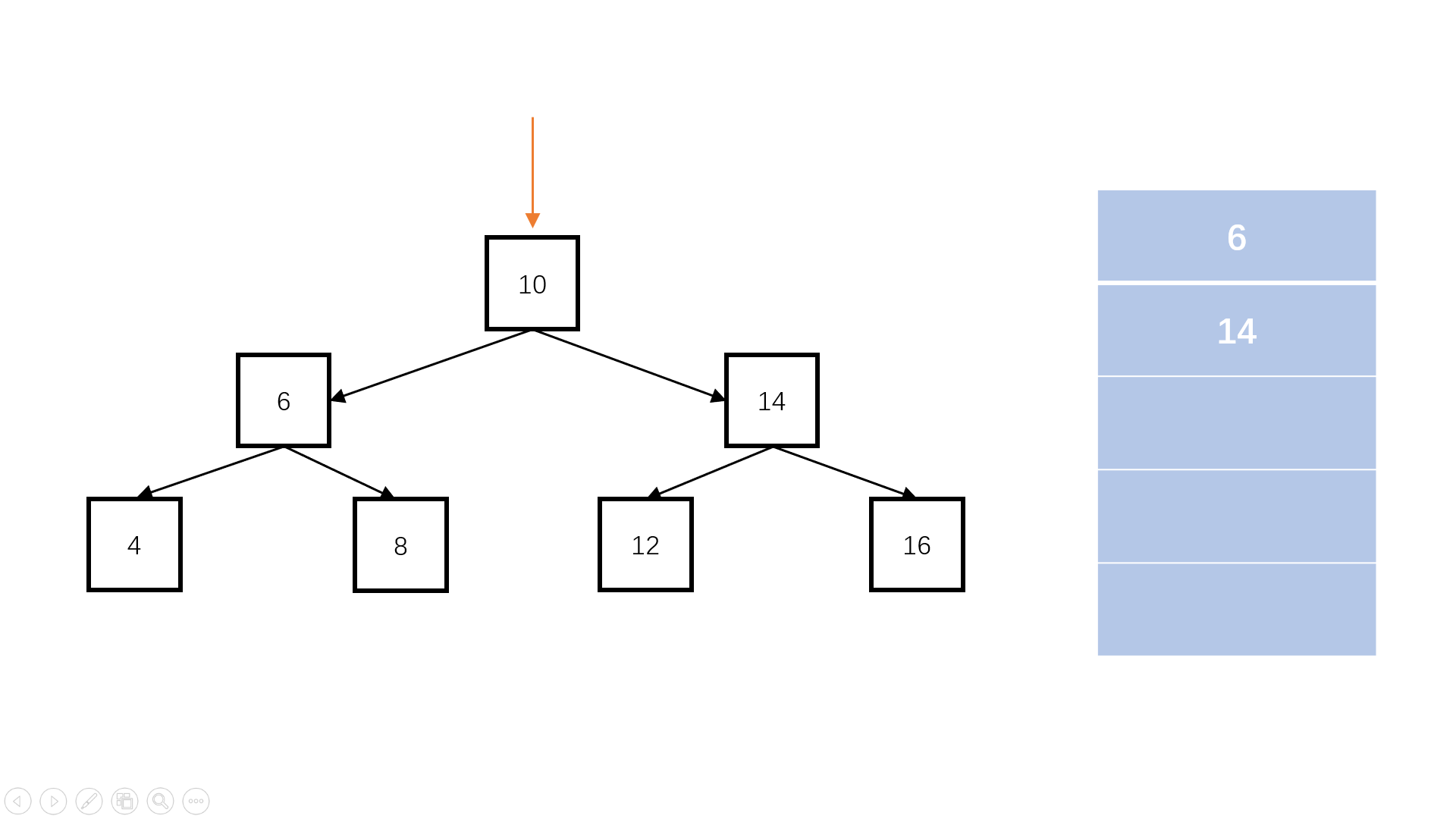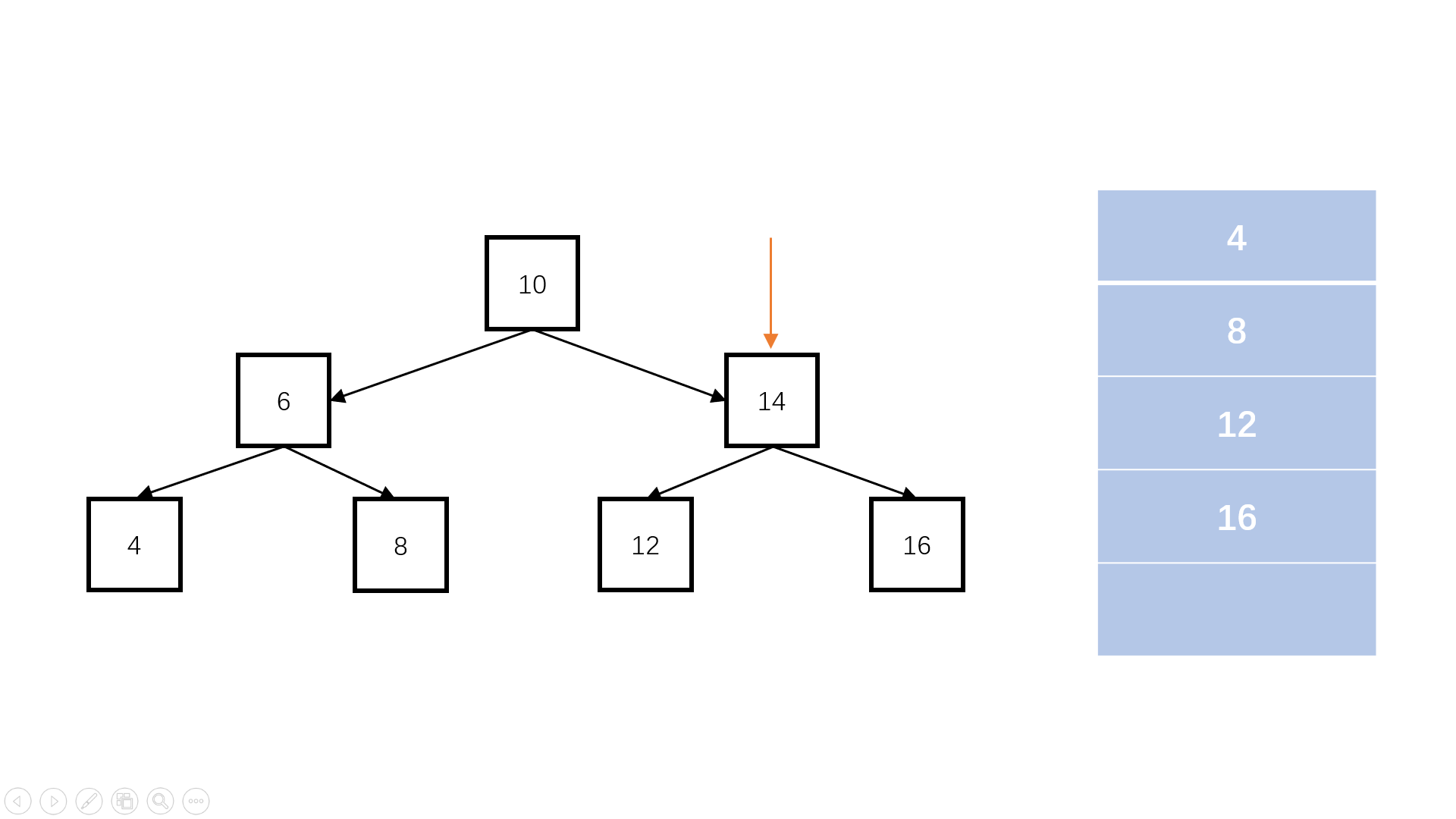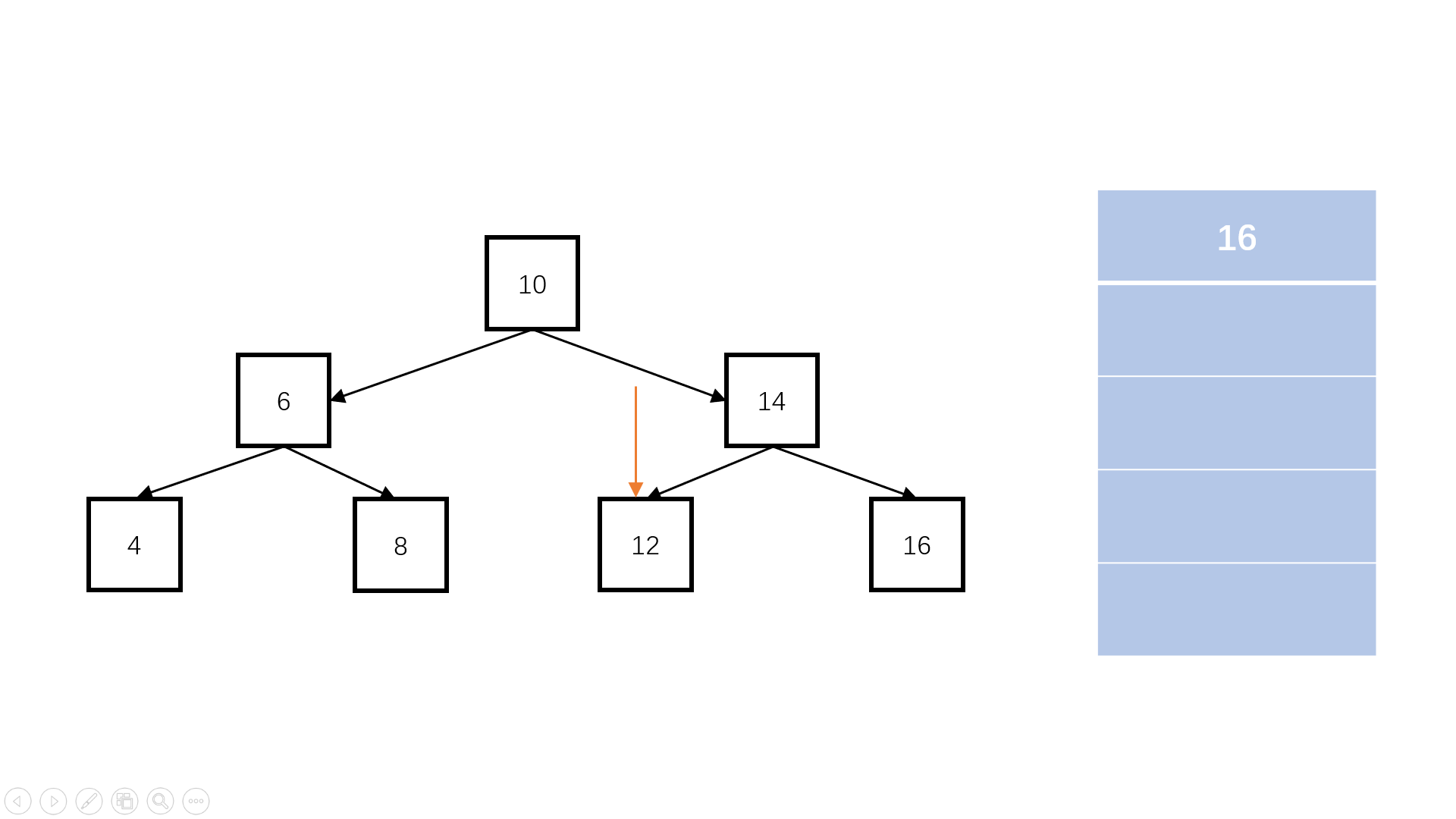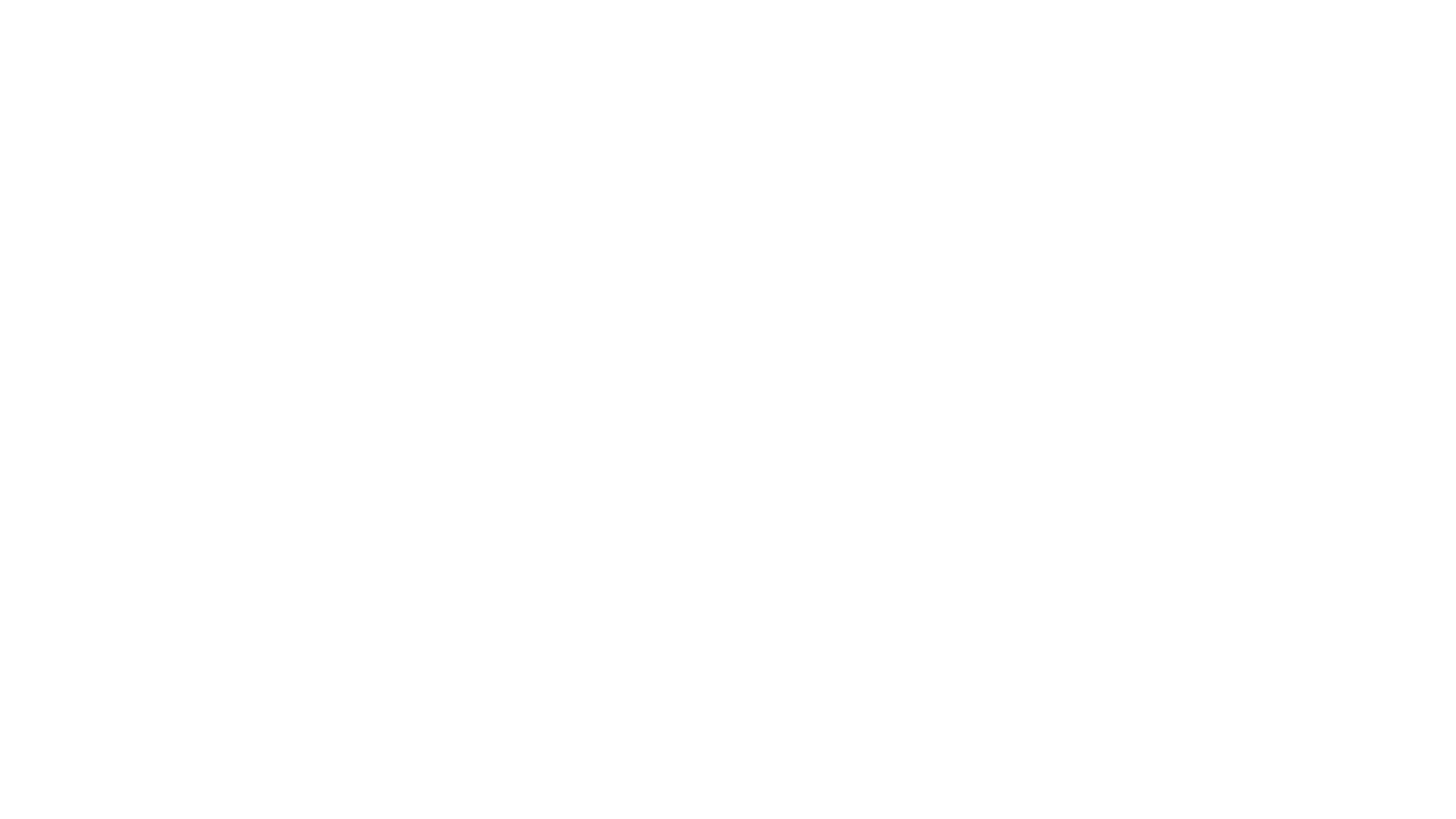
前序遍历:根节点、左子节点、右子节点
中序遍历:左子节点、根节点、右子节点
后序遍历:左子节点、右子节点、根节点
前序遍历 给你二叉树的根节点 root ,返回它节点值的前序遍历。
数据范围:二叉树的节点数量满足
Solution 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution {public :vector<int > preorderTraversal (TreeNode* root) {int > res;if (!root)return res;push (root);while (!container.empty ()) {auto node = container.top ();push_back (node->val);pop ();if (node->right) container.push (node->right);if (node->left) container.push (node->left);return res;
合并两个有序数组 给你两个按非递减顺序排列的整数数组 nums1 和nums2,另有两个整数 m 和n,分别表示 nums1 和nums2中的元素数目。
请你合并 nums2 到nums1中,使合并后的数组同样按非递减顺序排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1的初始长度为 m+n,其中前m 个元素表示应合并的元素,后 n 个元素为 0,应忽略。nums2 的长度为n。
示例 1:
输入:nums1=[1,2,3,0,0,0],m=3,nums2=[2,5,6],n=3[1,2,2,3,5,6][1,2,3] 和[2,5,6]。[1,2,2,3,5,6],其中斜体加粗标注的为nums1 中的元素。
示例 2:
输入:nums1=[1],m=1,nums2=[],n=0[1][1] 和[]。[1]。
示例 3:
输入:nums1=[0],m=0,nums2=[1],n=1[1][] 和[1]。[1]。m=0,所以nums1`` 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
Solution 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution {public :void merge (vector<int >& nums1, int m, vector<int >& nums2, int n) int i = m - 1 ;int j = n - 1 ;int p = m + n - 1 ;while (p >= 0 && j >= 0 ) {if (i < 0 ) {else if (nums2[j] >= nums1[i]) {else {swap (nums1[i], nums1[p]);
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution {public :void merge (vector<int >& nums1, int m, vector<int >& nums2, int n) int i = m - 1 ; int j = n - 1 ; int k = m + n - 1 ; while (i >= 0 && j >= 0 ) {if (nums1[i] > nums2[j]) {else {while (j >= 0 ) {
完全平方数 给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
示例 2:
输入:n = 13
思路及算法 我们可以依据题目的要求写出状态表达式:
这些数必然落在区间
其中
同时因为计算
Solution 1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution {public :int numSquares (int n) vector<int > f (n + 1 ) ;for (int i = 1 ; i <= n; i++) {int minn = INT_MAX;for (int j = 1 ; j * j <= i; j++) {min (minn, f[i - j * j]);1 ;return f[n];
把数字翻译成字符串 有一种将字母编码成数字的方式:’a’->1, ‘b->2’, … , ‘z->26’。
现在给一串数字,返回有多少种可能的译码结果
思路及算法 动态规划算法的基本思想是:将待求解的问题分解成若干个相互联系的子问题,先求解子问题,然后从这些子问题的解得到原问题的解;对于重复出现的子问题,只在第一次遇到的时候对它进行求解,并把答案保存起来,让以后再次遇到时直接引用答案,不必重新求解。动态规划算法将问题的解决方案视为一系列决策的结果
思路:
对于普通数组 1-9,译码方式只有一种,但是对于 11-19,21-26,译码方式有可选择的两种方案,因此我们使用动态规划将两种方案累计。
具体做法:
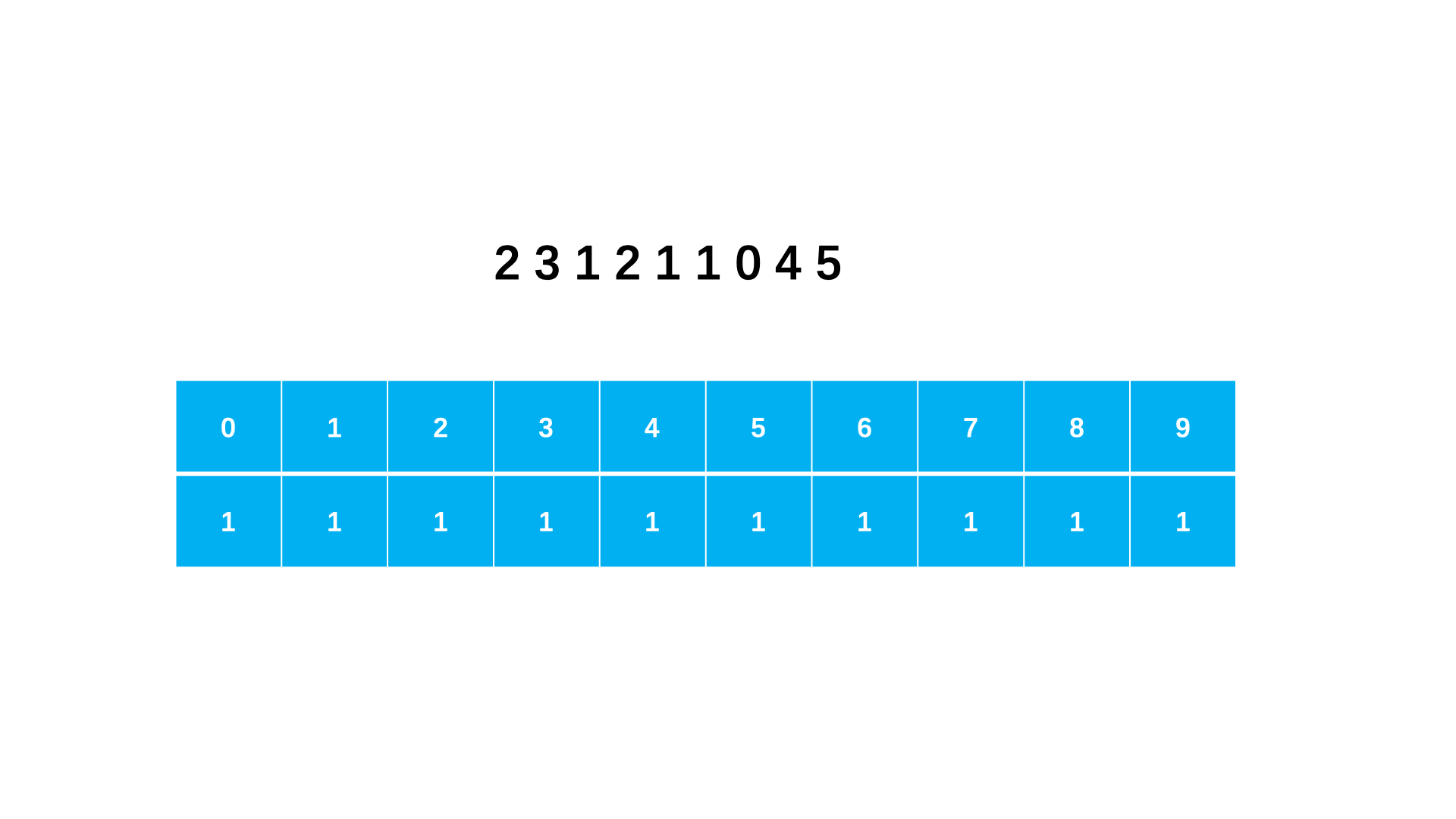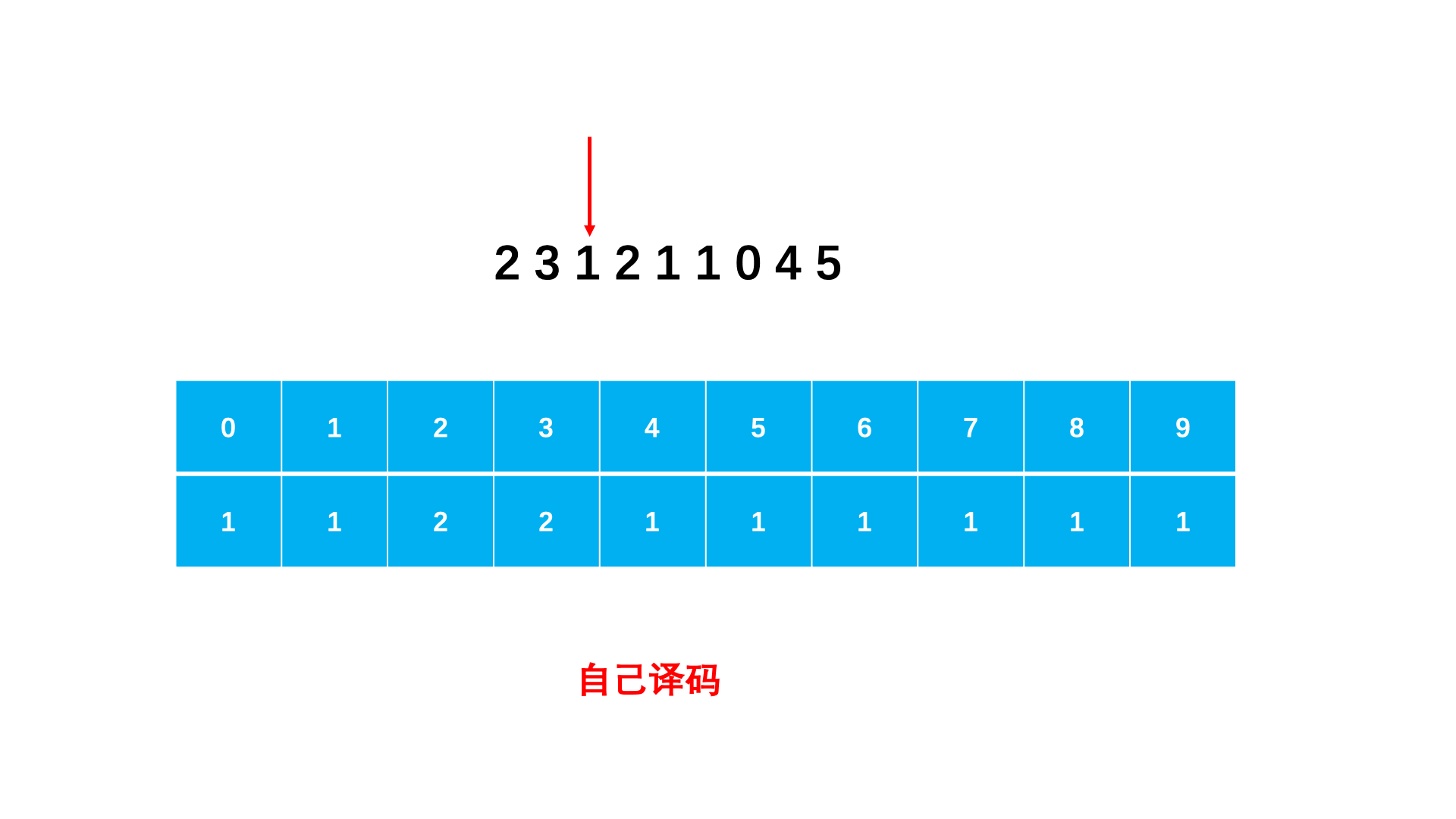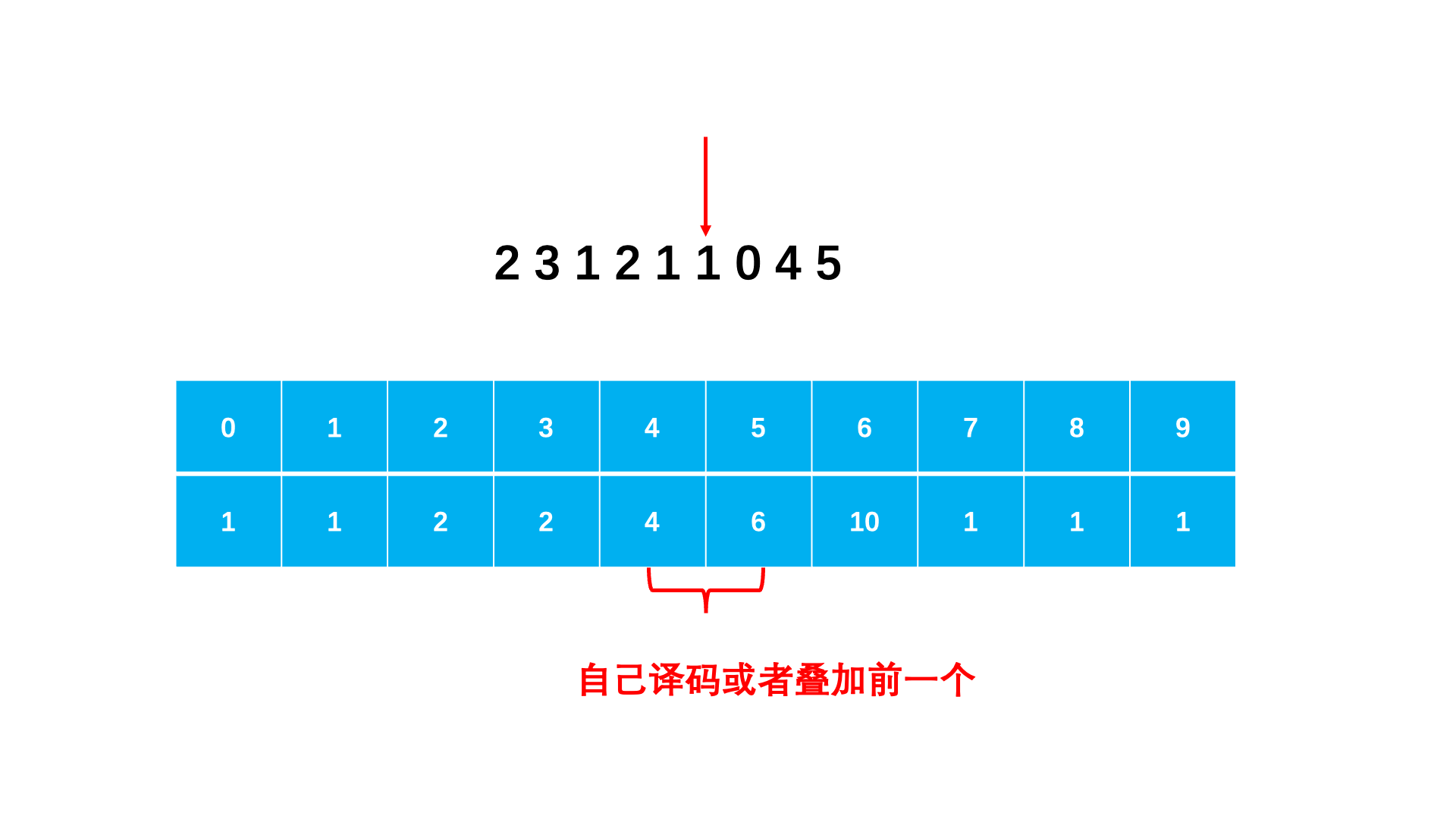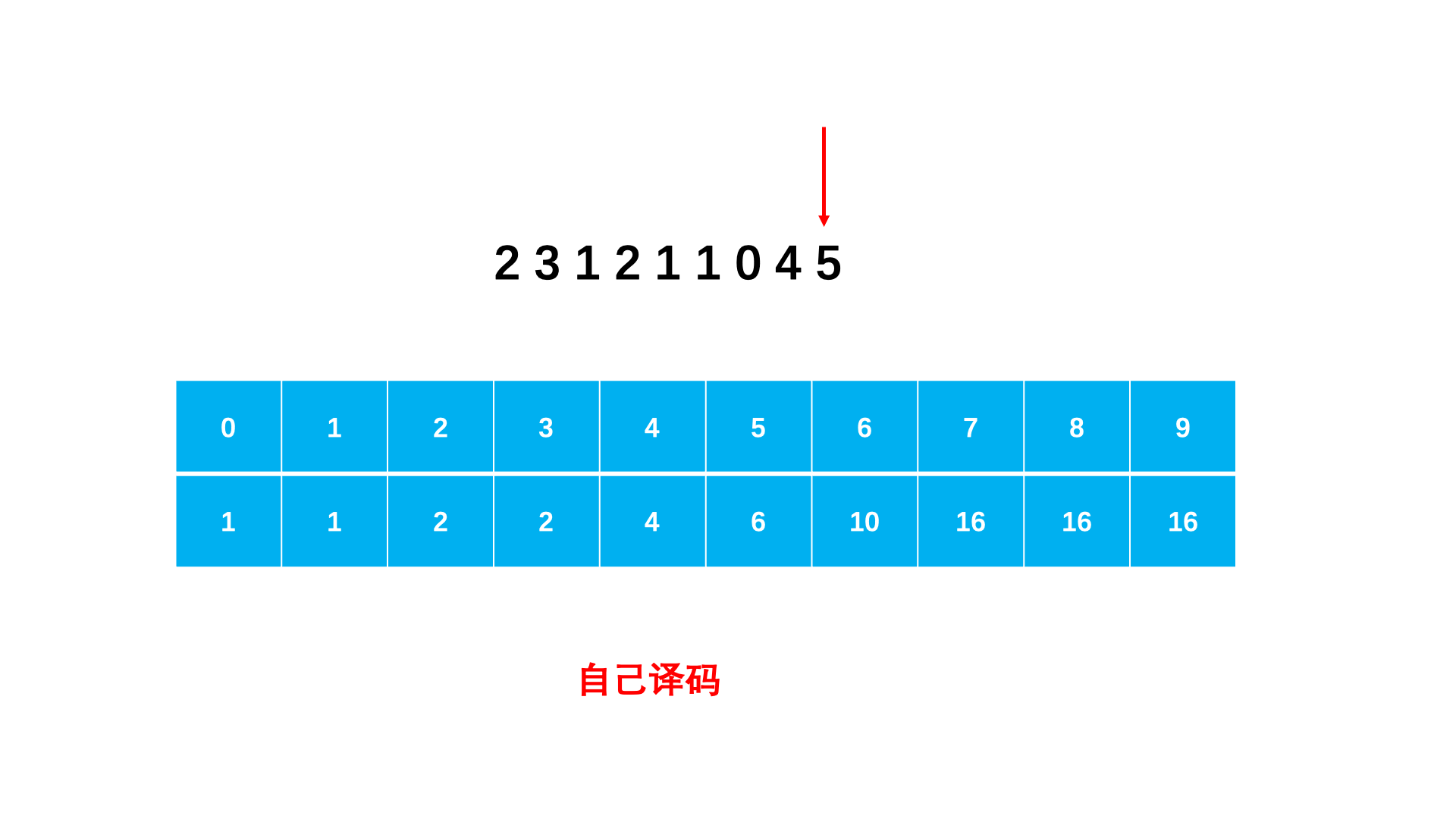
step 1:用辅助数组 dp 表示前 i 个数的译码方法有多少种。dp[i] = dp[i − 1];如果组合译码,则dp[i] = dp[i − 2]。dp[i−1] 即可,对于满足两种译码方式(10,20 不能)则是 dp[i − 1] + dp[i − 2]dp[length] 即为所求答案。
图示:
Solution 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution {public :int solve (string nums) if (nums == "0" ) return 0 ;if (nums == "10" || nums == "20" ) return 1 ;for (int i = 1 ; i < nums.length (); i++){if (nums[i] == '0' )if (nums[i - 1 ] != '1' && nums[i - 1 ] != '2' )return 0 ;vector<int > dp (nums.length() + 1 , 1 ) ; for (int i = 2 ; i <= nums.length (); i++){if ((nums[i - 2 ] == '1' && nums[i - 1 ] != '0' ) || (nums[i - 2 ] == '2' && nums[i - 1 ] > '0' && nums[i - 1 ] < '7' ))1 ] + dp[i - 2 ];else 1 ];return dp[nums.length ()];
最小区间 你有 k 个非递减排列的整数列表。找到一个最小区间,使得 k 个列表中的每个列表至少有一个数包含在其中。
我们定义如果 b - a < d - c 或者在 b - a == d - c 时a < c,则区间 [a, b] 比[c, d]小。
示例 1:
输入:nums = [[4,10,15,24,26], [0,9,12,20], [5,18,22,30]][20,24][4, 10, 15, 24, 26],24在区间 [20,24] 中。[0, 9, 12, 20],20在区间 [20,24] 中。[5, 18, 22, 30],22在区间 [20,24] 中。
示例 2:
输入:nums = [[1,2,3],[1,2,3],[1,2,3]][1,1]
思路 给定
假设这
由于
使用最小堆维护
如果一个列表的指针超出该列表的下标范围,则说明该列表中的所有元素都被遍历过,堆中不会再有该列表中的元素,因此退出循环。
Solution 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution {public :vector<int > smallestRange (vector<vector<int >>& nums) {int rangeLeft = 0 , rangeRight = INT_MAX;int size = nums.size ();vector<int > next (size) ;auto cmp = [&](const int & u, const int & v) {return nums[u][next[u]] > nums[v][next[v]];int , vector<int >, decltype (cmp)> pq (cmp);int minValue = 0 , maxValue = INT_MIN;for (int i = 0 ; i < size; ++i) {emplace (i);max (maxValue, nums[i][0 ]);while (true ) {int row = pq.top ();pop ();if (maxValue - minValue < rangeRight - rangeLeft) {if (next[row] == nums[row].size () - 1 ) {break ;max (maxValue, nums[row][next[row]]);emplace (row);return {rangeLeft, rangeRight};
Water 给定四个空杯子,容量分别为 S1 S2 S3 S4,允许进行以下操作:
将某个杯子接满水
将某个杯子里的水全部倒掉
将杯子 A 中的水倒进杯子 B,直到 A 倒空或者 B 被倒满
问最少要多少步操作才能使得这四个杯子装的水分别为 T1 T2 T3 T4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 输入例子:
Solution 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 #include <bits/stdc++.h> using namespace std;bool mem[64 ][64 ][64 ][64 ] = {false };bool equal (int s[4 ], int T[4 ]) return (s[0 ] == T[0 ]) && (s[1 ] == T[1 ]) && (s[2 ] == T[2 ]) && (s[3 ] == T[3 ]);int bfs (int S[4 ], int T[4 ]) int ,int ,int ,int >> q;auto x = make_tuple (0 , 0 , 0 , 0 );push (x);0 ][0 ][0 ][0 ] = true ;int step = 0 , cap[4 ] = {0 };while (!q.empty ()) {int size = q.size ();while (size--) {tie (cap[0 ], cap[1 ], cap[2 ], cap[3 ]) = q.front (); q.pop ();if (equal (cap, T)) {return step;for (int i = 0 ; i < 3 ; ++i) {switch (i) {case 0 : for (int j = 0 , tmp = 0 ; j < 4 ; ++j){make_tuple (cap[0 ], cap[1 ], cap[2 ], cap[3 ]);if (!mem[cap[0 ]][cap[1 ]][cap[2 ]][cap[3 ]]) {0 ]][cap[1 ]][cap[2 ]][cap[3 ]] = true ;push (x);break ;case 1 : for (int j = 0 , tmp = 0 ; j < 4 ; ++j) {0 ;make_tuple (cap[0 ], cap[1 ], cap[2 ], cap[3 ]);if (!mem[cap[0 ]][cap[1 ]][cap[2 ]][cap[3 ]]) {0 ]][cap[1 ]][cap[2 ]][cap[3 ]]=true ;push (x);break ;case 2 : for (int j = 0 ; j < 4 ; ++j) {int tmp1,tmp2,need;for (int z = 0 ; z < 4 ; ++z){if (j == z) continue ;min (cap[j], S[z]-cap[z]);make_tuple (cap[0 ], cap[1 ], cap[2 ], cap[3 ]);if (!mem[cap[0 ]][cap[1 ]][cap[2 ]][cap[3 ]]) {0 ]][cap[1 ]][cap[2 ]][cap[3 ]] = true ;push (x);return -1 ;int main () int S[4 ] = {0 }, T[4 ] = {0 };0 ] >> S[1 ] >> S[2 ] >> S[3 ];0 ] >> T[1 ] >> T[2 ] >> T[3 ];if (S[0 ] == 0 && S[1 ] == 0 && S[2 ] == 0 && S[3 ] == 0 && !equal (S,T)) {-1 << endl;else {int ret = bfs (S, T);return 0 ;
分割后处理 研究地球空间科学的永强想研究海岸线的长度和海岸线面积之间的关系,为此他找来了很多航拍图像。在航拍图像上利用图像分割的方法,把图像的每个像素标记成陆地(1)和水面(0)。
示例图片:
现在永强想知道每张图中陆地部分的面积。
已知每张图最底部的一条边都是陆地,并且在一张图上陆地都是四邻域联通的。
但是永强发现分割的结果有很多的噪声,于是他定义了如下规则试图去除噪声:
如果一个水面区域被陆地包围,则将这个区域记为陆地;
在 a 的基础上如果一个陆地区域不和底边的陆地相连,那么这是一个岛屿,不计入陆地的面积。
1 2 3 4 5 6 7 8 9 10 输入例子:
思路
此时岛屿标记为 1,水标记为 2,陆地标记为 3
Solution 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 #include <bits/stdc++.h> using namespace std;int result = 0 ;void surround (vector<vector<int >>& pic, int i, int j) if (i < 0 || i >= pic.size () || j < 0 || j >= pic[0 ].size () || pic[i][j] == 1 || pic[i][j] == 2 ) return ;2 ;int dx[4 ] = {-1 , 1 , 0 , 0 };int dy[4 ] = {0 , 0 , -1 , 1 };for (int k = 0 ; k < 4 ; k++) {surround (pic, i + dx[k], j + dy[k]);void cal_area (vector<vector<int >>& pic, int i, int j) if (i < 0 || i >= pic.size () || j < 0 || j >= pic[0 ].size () || pic[i][j] == 2 || pic[i][j] == 3 ) return ;3 ;int dx[4 ] = {-1 , 1 , 0 , 0 };int dy[4 ] = {0 , 0 , -1 , 1 };for (int k = 0 ; k < 4 ; k++) {cal_area (pic, i + dx[k], j + dy[k]);int main () int m, n;int >> pic (m, vector <int > (n, 0 ));for (int i = 0 ; i < m; i++) {for (int j = 0 ; j < n; j++){for (int i = 0 ; i < m; i++) {for (int j = 0 ; j < n; j++){bool edge = i == 0 || i == m - 1 || j == 0 || j == n - 1 ;if (pic[i][j] == 0 && edge) {surround (pic, i, j);for (int i = 0 ; i < m; i++) {for (int j = 0 ; j < n; j++){if (pic[i][j] == 0 ) {1 ;for (int i = 0 ; i < m; i++) {for (int j = 0 ; j < n; j++){bool bottom = i == m - 1 ;if (pic[i][j] == 1 && bottom) {cal_area (pic, i, j);return 0 ;
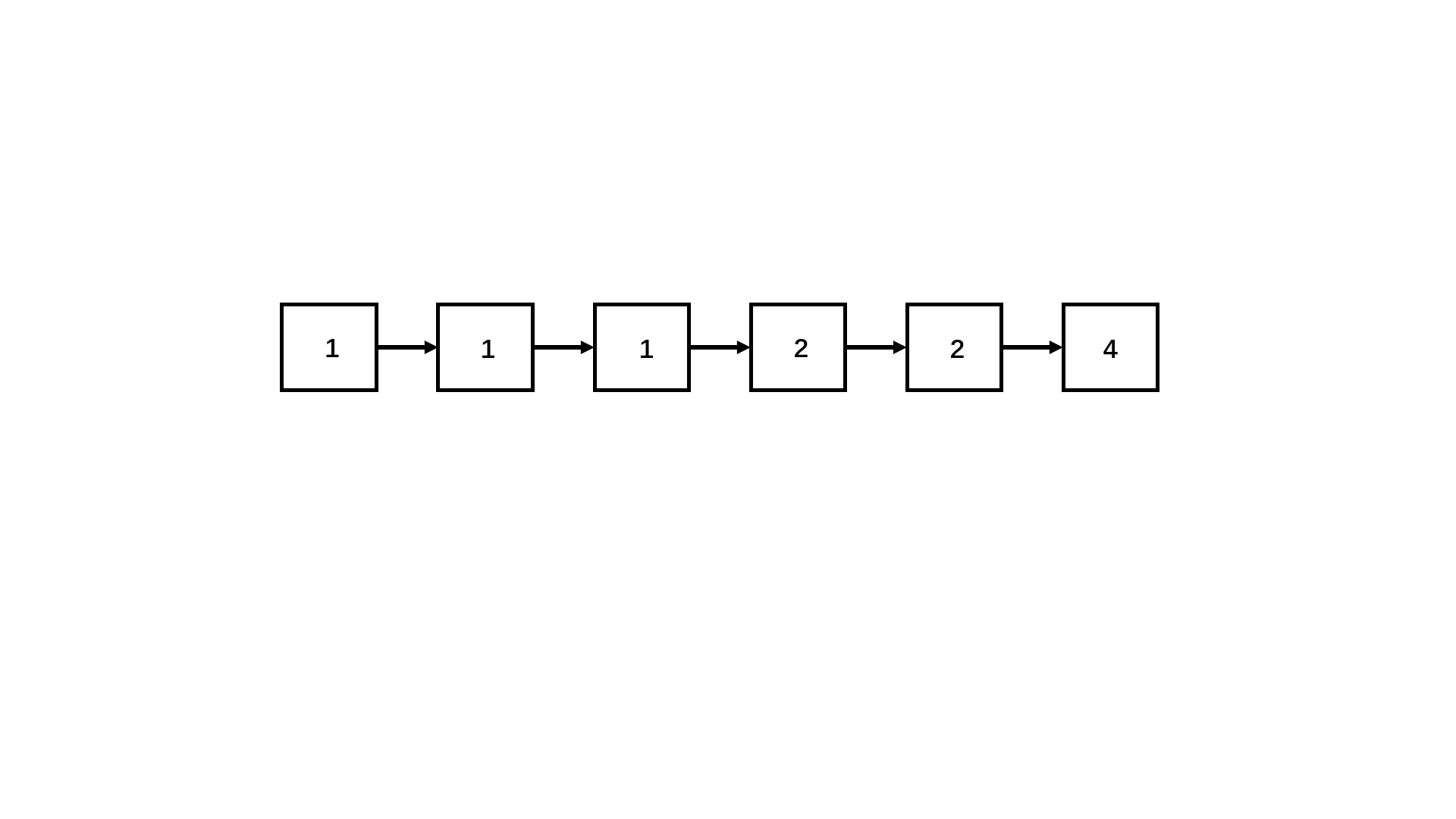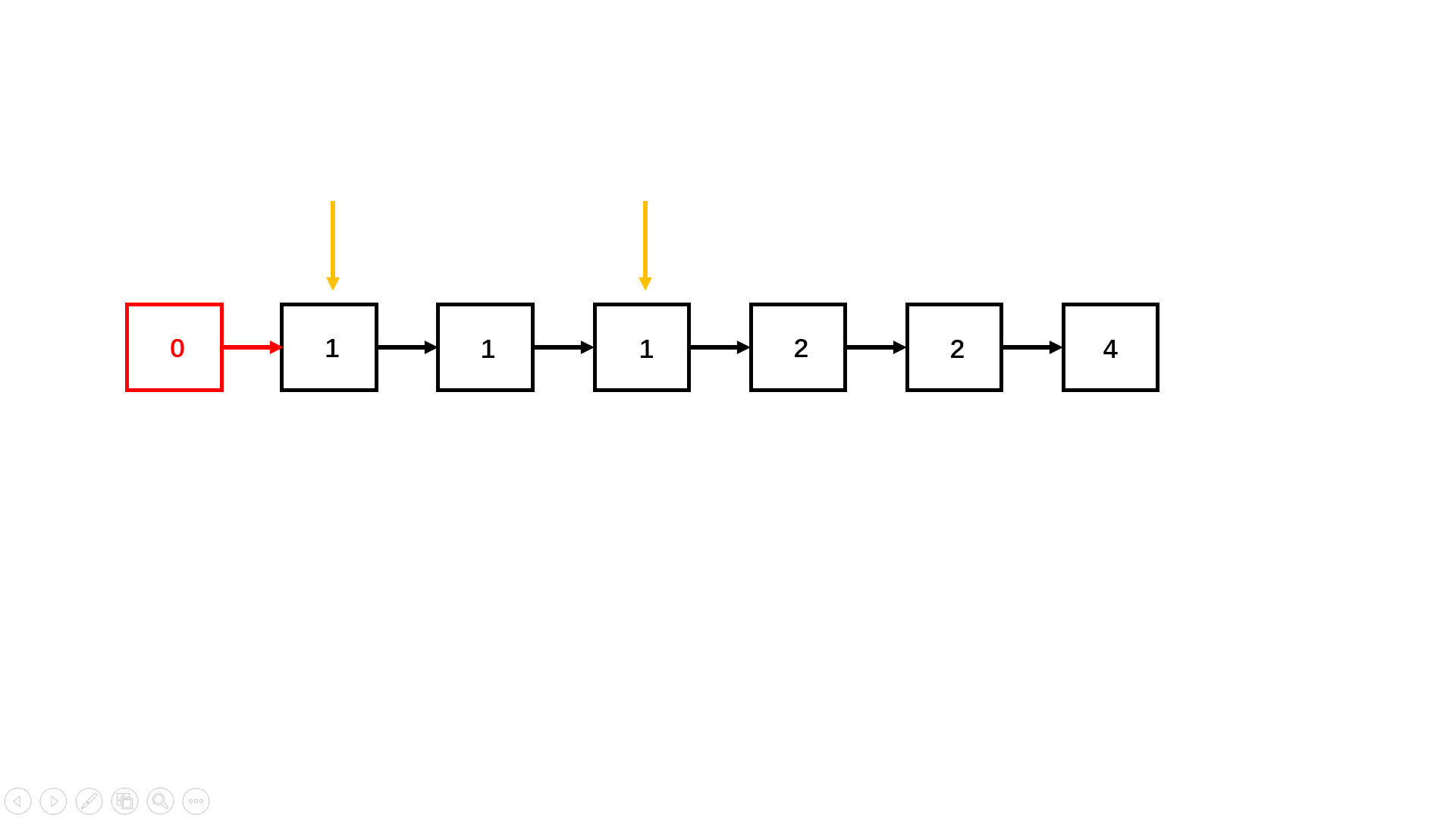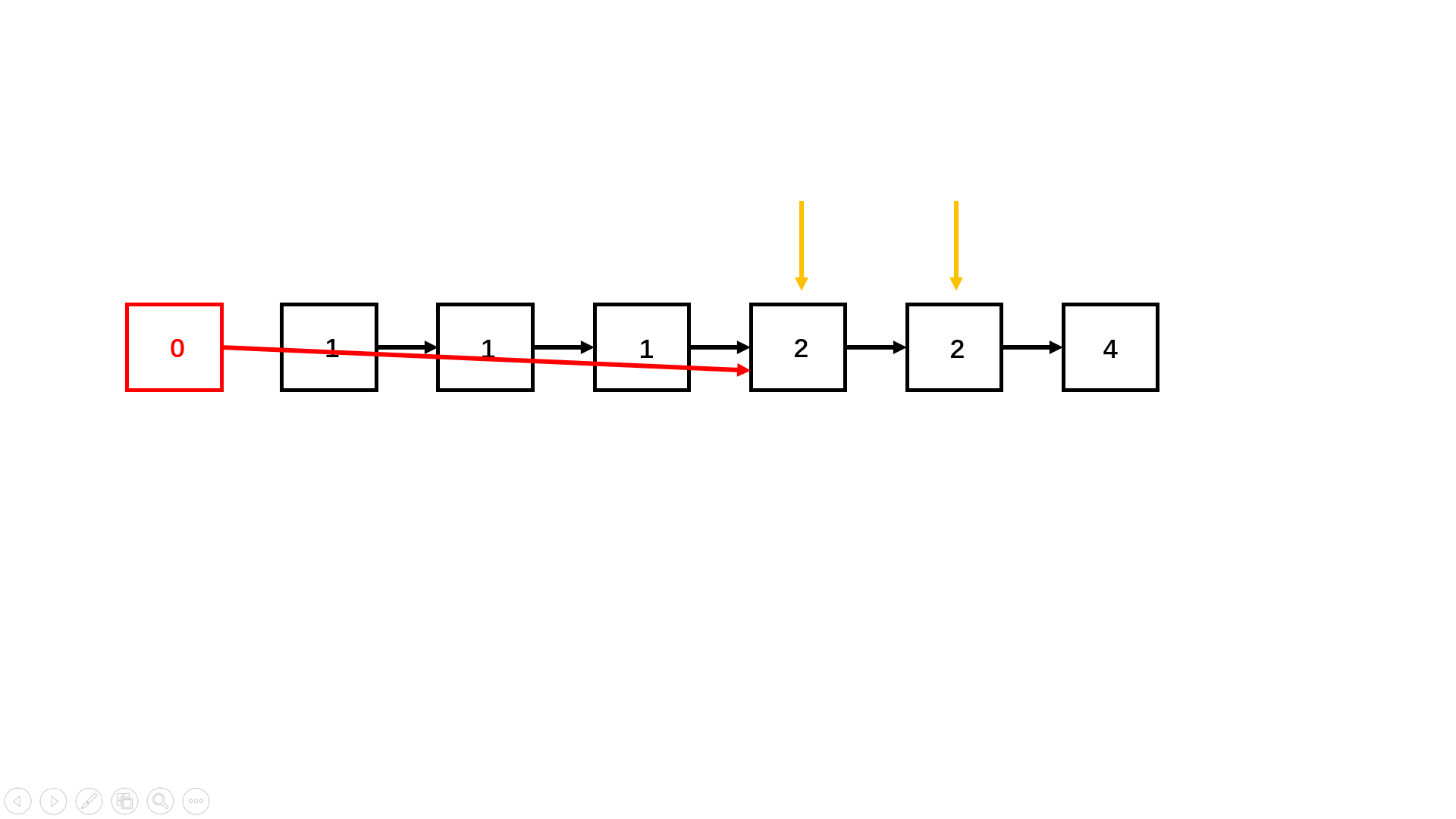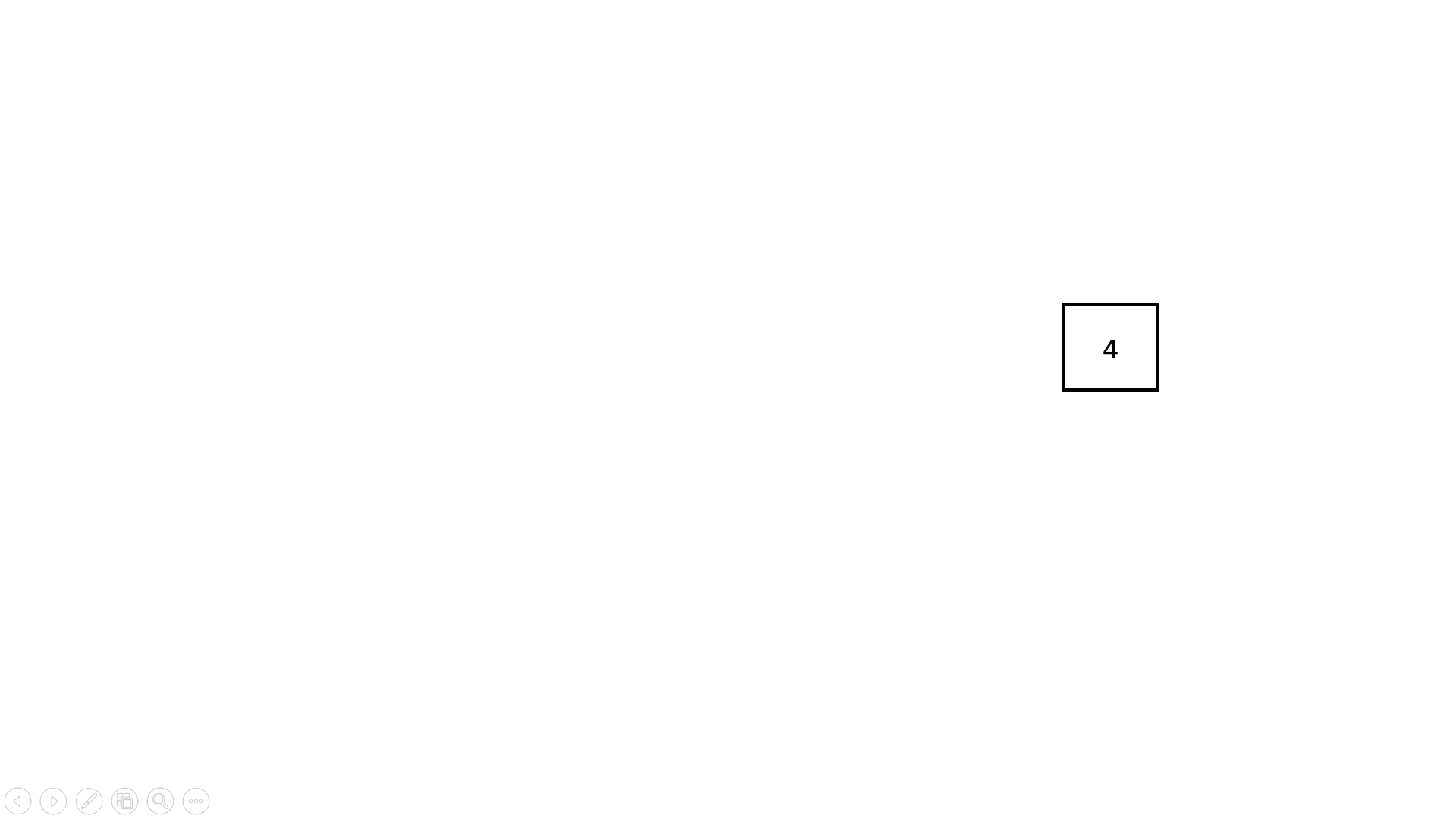
删除有序链表中重复的元素 I 删除给出链表中的重复元素(链表中元素从小到大有序),使链表中的所有元素都只出现一次 1 → 1 → 2, 返回1 → 21 → 1 → 2 → 3 → 3, 返回1 → 2 → 3
Solution 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution {public :ListNode* deleteDuplicates (ListNode* head) {if (head == nullptr )return head;auto p = head;auto q = p->next;while (q) {if (p->val == q->val) {else {return head;
II 给出一个升序排序的链表,删除链表中的所有重复出现的元素,只保留原链表中只出现一次的元素。1 → 2 → 3 → 3 → 4 → 4 → 5, 返回1 → 2 → 51 → 1 → 1 → 2 → 3, 返回2 → 3
Solution 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 class Solution {public :ListNode* deleteDuplicates (ListNode* head) {if (head == nullptr )return head;auto p = head;auto q = head->next;if (q == nullptr )return head;auto * h = new ListNode (0 );while (q) {if (p->val != q->val) {else {while (q && q->val == p->val) {if (q) q = q->next;return head->next;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class Solution {public :ListNode* deleteDuplicates (ListNode* head) {if (head == NULL ) return NULL ;new ListNode (0 );while (cur->next != NULL && cur->next->next != NULL ){if (cur->next->val == cur->next->next->val){int temp = cur->next->val;while (cur->next != NULL && cur->next->val == temp) else return res->next;
岛屿数量 给一个 01 矩阵,1 代表是陆地,0 代表海洋, 如果两个 1 相邻,那么这两个 1 属于同一个岛。我们只考虑上下左右为相邻。
Solution 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 class Solution {public :void dfs (int i, int j, size_t height, size_t width, vector<vector<char >>& grid) '0' ;if (i + 1 < height && grid[i + 1 ][j] == '1' ) {dfs (i + 1 , j, height, width, grid); }if (j + 1 < width && grid[i][j + 1 ] == '1' ) {dfs (i, j + 1 , height, width, grid); }if (i - 1 >= 0 && grid[i - 1 ][j] == '1' ) {dfs (i - 1 , j, height, width, grid); }if (j - 1 >= 0 && grid[i][j - 1 ] == '1' ) {dfs (i, j - 1 , height, width, grid); }int solve (vector<vector<char > >& grid) int res = 0 ;size_t height = grid.size ();if (height == 0 )return 0 ;size_t width = grid[0 ].size ();for (auto i = 0 ; i < height; i++) {for (auto j = 0 ; j < width; j++) {if (grid[i][j] == '1' ) {dfs (i, j, height, width, grid);return res;
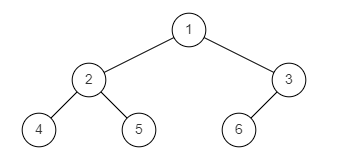
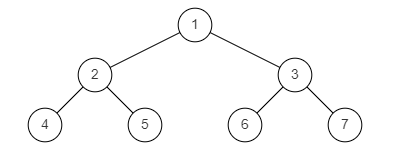
判断是不是完全二叉树 给定一个二叉树,确定他是否是一个完全二叉树。
完全二叉树的定义:若二叉树的深度为
Solution 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution {public :bool isCompleteTree (TreeNode* root) if (!root) return true ;if (root->left && (!root->left->left || !root->left->right) && root->right && (root->right->left || root->right->right)) return false ;if (root->left && root->left->left && !root->right) return false ; if (!root->left && root->right) return false ; return isCompleteTree (root->left) && isCompleteTree (root->right);
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution {public :bool isCompleteTree (TreeNode* root) if (root == NULL ) return true ;push (root); bool flag = false ; while (!q.empty ()){int sz = q.size ();for (int i = 0 ; i < sz; i++) {front ();pop ();if (cur == NULL ) true ; else {if (flag) return false ;push (cur->left);push (cur->right);return true ;