Markov Decision Processes
Basics
- 有的地方写作
: state space, : initial state - 在代码就是
s0 = mdp.reset()
- 在代码就是
: action space, applicable in each state 当前状态 下允许的动作 转移概率(trasition probabilities),对于 - 也可以写作:
- 是概率化的(即 probabilistic state model),而非确定性的(deterministic)的
- 如果是确定性的,那就是一个经典的序列决策问题了
- 也可以写作:
: reward function,可以为正(奖励);也可以为负(惩罚) - 设计一个 MDP 环境,很大一部分是在设计 reward function
: 确定性的情况下 : 是在不确定的情况下产生的奖励,就好像抛硬币,不知道下一次出现的是正面还是反面,这时就需要用概率分布来计算了
: discount factor - 一般又把这种 MDP 称之为 discounted reward MDP
- MDP 的求解是一个序列决策问题(sequence decision making)
Probabilistic State Model
- 抛硬币:正面朝上的概率是
,反面朝上的概率也是 - 掷 2 个骰子计算点数和:和为 2 的概率是
,和为 2 的概率是 ,和为 4 的概率是 , ,和为 12 的概率是 - 机械臂去拿一个东西:成功的概率是
,失败的概率是 - 打开一个网页:404 的概率 1%,200 的概率 99%
Discounted Reward
如果 agent 在与环境交互中得到一些列的 reward
,则有 - 递归定义,体现子问题的结构(可以使用动态规划)
的价值通过 折到现在 - 因为要最大化 discounted reward,所以
会隐式地得到一个更短路径 - 另外一个角度是:aciton 会有 cost
Grid World
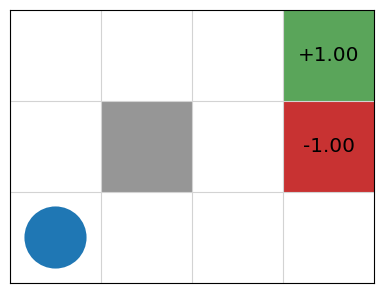
Markov Decision Processes
https://silhouettesforyou.github.io/2024/07/30/990e4273260f/